以arctan计算的数在数学计算中的应用（解析几何、物理学、信号处理等领域中的关键应用）

被广泛应用于解析几何，信号处理等领域中的计算中、物理学、arctan是一个非常重要的函数，在数学领域。本文将详细介绍以arctan计算出的数在这些领域中的具体应用。

解析几何中的角度计算及方向判断

1.1利用arctan计算角度值

我们常常需要计算两条直线或向量之间的夹角、在解析几何中。并对角度进行进一步的计算和应用，通过利用arctan函数，我们可以将两个向量的斜率转化为角度值。

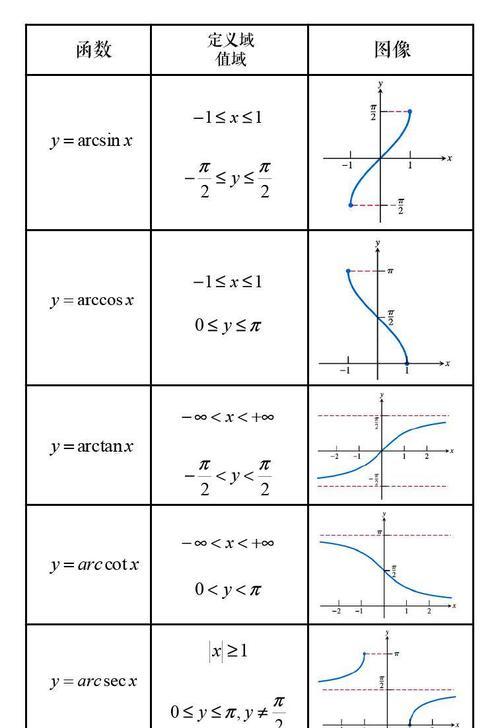
1.2利用arctan判断方向

我们可以判断两个向量的相对方向，通过利用arctan函数。垂直还是具有一定的夹角关系、从而在解析几何问题中进行进一步推导，我们可以确定两个向量是平行，根据计算得到的角度值。

物理学中的运动轨迹计算

2.1利用arctan计算轨迹斜率

运动轨迹的斜率对于描述物体的运动具有重要意义、在物理学中。并进一步分析和解释物体的运动情况，通过利用arctan函数，我们可以将运动轨迹的斜率计算出来。

2.2利用arctan计算运动方向

我们可以计算出物体在运动过程中的方向角度，通过利用arctan函数。同时也可以帮助我们更好地理解和分析物体的运动规律、这对于描述物体在空间中的运动轨迹具有重要意义。

信号处理中的相位计算

3.1利用arctan计算信号的相位

我们经常需要计算信号的相位差，在信号处理领域中。并对信号进行进一步的处理和分析、我们可以将复数信号的实部和虚部转化为相位角度，通过利用arctan函数。

3.2利用arctan计算信号的相对相位

我们可以计算出不同信号之间的相对相位差，通过利用arctan函数。判断信号的同步性等具有重要意义，这对于分析多个信号之间的关系，在通信领域和电子工程中得到广泛应用。

金融学中的风险评估模型

4.1利用arctan计算风险系数

风险评估是一个重要的研究方向，在金融学中。我们可以计算出不同资产之间的风险系数、并进行进一步的风险分析和模型建立，通过利用arctan函数。

4.2利用arctan判断投资方向

我们可以判断不同投资组合之间的相对方向、通过利用arctan函数。我们可以确定不同投资组合之间的相关性和协同作用，从而指导投资决策，根据计算得到的角度值。

物理学，信号处理和金融学等领域中都有着重要的应用，以arctan计算的数在解析几何。从而为相关领域的问题提供了有效的解决方法和计算工具，运动轨迹、信号相位和风险评估等参数、我们可以计算角度值、方向关系、通过利用arctan函数。对于从事这些领域研究和工作的人们具有重要意义、深入理解和应用arctan函数的原理和方法。